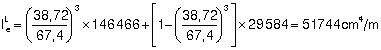INDEX

• Introduction
• 1^st case: Flat slab
• 2^nd case: Waffle slab with lost forms

Introduction

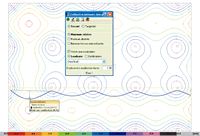
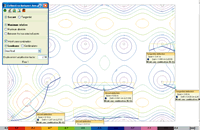
Upon marking an initial and final point on the plan view of a flat or waffle slab, a continuous yellow line appears joining the two points displaying the vertical displacements of all the points creating an approximately sinuous curve below the line. The blue curve displays the deformed shape of the slab, for a simple loadcase, combination or worst case combination (G+Q) with amplified displacements.

When the floor layout of the supports is visible on screen and the two points to calculate the deflection are marked, the user can observe that convex distributions are present in the support zones whereas at span centres concave distributions are visible.
Let us study what occurs in the case of displacements in the Z direction (vertical) corresponding to the combination G+Q of the permanent load G loadcase ( which usually represents the greatest percentage) and live load Q loadcase to observe where the maximum values are produced. At a first glance, looking at the displacement contour lines, the maximum values coincide with the areas with greatest concave distributions.

In the case of a two-way spanning slab, we do not know beforehand whether the area with greatest concave distribution corresponds to that of themaximum absolute deflection. It is logical to think it should be, as the descent of the supports is generally small, and we should concentrate on those areas where these maximum values can be seen. There is also the uncertainty as to in which direction (X, Y, diagonal) the points should be marked to obtain the maximum relative deflection. However, one could say, from observing the layout of a floor, that it should be in the direction of the smallest distance between two points of the concave distribution perimeter.

It is recommended it generally be done in this manner.

To find the edges of the concave distribution perimeters, it may be useful to previously select points which lie further away so to find their position.

Let us carry out a few simple examples so to clarify what has been explained. The data is as follows:

• Mean span = 6,50 m
• External span
• Approximate moment distribution

Negative moment internal support
Positive moment for span
Negative moment external support

• Partitions = 1 kN/m²built after 60 days (2 months)
• Screed = 1 kN/m²laid after 120 days (4 months)
• Live load = 2 kN/m²
• Materials = HA-25 (fck=25 MPa)  y B500 (fyk=500 MPa), mean temperature and humidity conditions during building process and use.

1^st case: Flat slab

Let us estimate a depth of 26 cm, whose slenderness is L/h = 650/26 = 25, Its deflection has to be checked. According to table 50.2.2.1.a of the Spanish EHE-08 code, the value for the slenderness is 23 (for weakly reinforced elements) and so its verification must be justified.

Let us carry out an approximate analysis on a metre wide section, with the aforementioned properties and to obtain the forces acting on it. Even though the support distribution is that of a flat slab with isolated supports, we shall assume there are uniform supports so to simplify the analysis.

The gross inertia of the section of the flat slab is , therefore  in our case. The stiffness of the model can be calculated using this value and the instantaneous elastic displacements for each selected loadcase and combination are obtained.

To establish the deflection between two points based on the displacements, the displacements of the initial and final points must be deducted.

The graph shows a line which passes through those two points (secant) or a line at a tangent to the initial point (tangential), depending on the section carried out. The deflection is measured with respect to that line.

The values displayed are:

• Span L
• Absolute deflection
• Relative deflection with respect to: L (secant); 2L (tangent)
• Worst case combination G+Q obtained from the selected “Displacements” combinations in the general data section of the job. Only gravitational loadcases G and Q are considered (activated by default). It may also be selected by loadcase or combination loadcase.

A “Displacement amplification factor” = 2.50 (default value) is displayed. This does exactly as it says; multiplies the displacements due to that loadcase by that value and displays the result. This amplification factor should be incorporated and all the parameters relative to the following be taken into account:

• Period of formwork removal
• Construction process
• Thermal phenomenon
• Rheological phenomenon (creep, retraction)

Once the instantaneous elastic deflection is known, the total deflection or active deflection (after the damageable elements have been built, for example partitions or rigid paving without joints)  can be found, by estimating the aforementioned parameters. By placing the adequate value, the deflection sought will be obtained and so can be compared with the limits stated in the code.

Assuming a usual construction process, with the corresponding building loads:

• Self weight of the slab (h=26 cm) = 6,5 kN/m²unpropped after 28 days (1 month)

Using the laws applicable to an external span (as if virtual frames were to be applied), the bending moment diagram and the required reinforcement per metre width can be found.

Hence providing an approximate area,

Now to calculate the cracking moment:

Where f_ct,m,fl: mean tensile bending resistance of the concrete
f_ct,m: mean tensile resistance of the concrete

An added safety factor is applied by considering the service moments due to the total load:

To determine the cracked inertia I_crack y and Branson’s equivalent inertia I_e :

where:
I_e: equivalent inertia
M_crack: cracking moment
M_a: moment acting on the section
I_g: gross inertia
I_crack: cracked inertia

This is done in the 3 sections under study:

And the mean equivalent inertia of the span will be determined :

Where

To be on the safe side and by reducing the equivalent inertia to , a correction coefficient due to the cracking of the sections is to be applied to the elastic deflection provided by the program. This coefficient K_e, has a value of:

If the method described in the Spanish EHE-08 code (similar to ACI-08), where the differed deflection is assumed to be proportional to the instantaneous deflection by a factor λ whose value is:

ξ: coefficient which depends on the time or duration of the load
ρ: mean area of reinforcement in compression

If a top and bottom mesh is provided which will cover, for example 1‰ (ρ = 0,001), ξ will take the following values:

t	ξ
∞ ≥ 5 years	2,0
1 year	1,4
6 months	1,2
1 month	0,7
2 weeks	0,5

Let us now look at the construction process and the deflections that are produced.

First of all, assume the total deflection:

Permanent load	Value	t	ξ	ξ = ξ (∞) - ξ (t)     t: when load begins to act
	kN/m2	days
Self weight	6,5	28	2-0,7 = 1,3
Partitions	1,0	60	2-0,8 = 1,2
Screed	1,0	120	2-1 = 1
Live loads	2	365	2-1,4 = 0,6

With the assumed live load, only the quasi-permanent part produces differed deflection (for dwellings Y2=0,3). By applying it to the total:

Now,

To obtain the instantaneous deflection corrected by the reduction of the inertia due to cracking, the value of the instantaneous deflection δ_i is multiplied by K_e:

δ_inst = K_e · δ_i = 1,50 δ_i

On the other hand, for the total differed deflection a coefficient of λ = 1,00 has been obtained, hence

δ_dif = λ ·  δ_inst  = 1,00 · δ_inst

and the total deflection is:

δ_Total = δ_inst + δ_dif = 1,5 δ_i + 1,00 x 1,5 δ_i = 3,00 δ_i

This value of 3,00 is precisely that coefficient which is presented as “Displacement amplification factor” (whose default value is set at 2,5)

CYPECAD’s user’s manual mentions that this value can lie between 2,5 and 3,0, depending on the construction process.

For this example the value obtained has been 3,00, amount which is to be introduced in the dialogue box to consult the total deflection and view the selected results between two points.

Similarly, to determine the active deflection, in this case, that which arises after the damageable element has been built, the deflection which occurs before it is built must be subtracted. In this example, the instantaneous deflection due to the self weight of the slab and the differed deflection since removing the props until the partitions were built after 60 days have to be removed. Hence ξ_s.weight = (2- 0,8) = 1,2, and so:

Therefore the differed deflection will be δ_dif = 0,93 δ_inst.

Regarding the instantaneous deflection to be considered, the corresponding part due to the self weight must be removed. Hence by the proportion of the loads without the self weight to the total loads:

Therefore:

This would be the value to introduce in the “Displacement amplification factor” box to obtain the active deflection.

Obviously, it can be seen that for the foreseen loads and construction periods, by rounding off to whole values, a flat slab has an active deflection of approximately 2,0 times the instantaneous elastic deflection established using the gross section and a total deflection of approximately 3,0 times that instantaneous deflection.

2^nd case: Waffle slab with lost forms

A similar estimate will now be undertaken for a waffle slab introduced in CYPECAD.

The lost form waffle slab for this example will have the following geometry:

Having found the centre of gravity of the section, the inertia of the gross section with respect to this centre of gravity can be calculated:

By repeating the same process with the drop panel zone, it can be seen that it resembles a flat slab with a depth of 30 cm and a width of 82 cm:

The mean inertia of the section along its span could be estimated to be:

In the CYPECAD model, the inertia applied to all the mesh of a panel of any waffle slab, be it in the lightweight or solid zone, is the same and is taken as half of that of the solid zone, which in this case is:

and it is with this inertia that the elastic displacements for each loadcase are found.
The next step would be to verify whether the sections crack or not due to the forces acting on it and establish the equivalent inertia.

For the solid zone and taking a width = 0,82 m, the cracking moment is:

and for the lightweight zone:

Let us estimate the moments acting on the structure:

Slab self weight:	4,6 kN/m2	(*)
Partitions:	1,0 kN/m2
Screed:	1,0 kN/m2
Live load:	2,0 kN/m2 8,6 kN/m2

(*) The lightweight zone has been considered, as the solid zone has little influence on the acting moments.

The moments for hypothetically supported rib would be:

It can be seen that there is very little cracking in the negative moment zones, however there is in the positive moment zone of the span.

The equivalent inertia of the span can be estimated as:

For the right support, it shall be taken equal to the gross section:

and for the left support:

By taking the average:

As the inertia considered in the analysis , no correction will be applied, however for greater safety the equivalent inertia , will be taken and so amplifying by

Regarding , we will assume (to be on the safe side) that ρ =  0, hence λ = ξ, with and the same construction process and durations will be present. Therefore:

It can be said that the differed deflection is approximately equal to the instantaneous deflection (δ_dif ≈δ_inst = 1,25 fδ); and the total deflection is:

As δ_inst = 1,25 δ_i

Now to obtain the differed deflection after the partitions have been built:

and the instantaneous deflection must be left without the self weight of the slab:

hence the active deflection will be:

It can be said that the total long-term deflection for a waffle slab must be obtained with a displacement amplification factor of the order of 2,5 times the instantaneous elastic deflection of the program, and for the active deflection, the user would have to multiply the instantaneous elastic deflection by 1,75.

It must be taken into account that the indicated coefficients are those applied to usual building cases such as those mentioned regarding, span lengths, depths, loads, construction procedure, normal environment conditions, unpropping periods, and entering into force of the loads in time.

If these conditions are varied, then logically the pertinent correction coefficients have to be applied.

If the deflection to be verified is that for comfort, it will be sufficient if the deflection due to the live loads in loadcase LL are analysed.

SUMMARY TABLE